| Attention | Topic was automatically imported from the old Question2Answer platform. | |
| Asked By | Shep |
Hi,
I have an issue with the normal from collision.normal
Given this piece code :
extends KinematicBody2D
var velocity : Vector2 = Vector2()
var move_speed : int = 60
func _ready():
velocity = Vector2(3, 6) * move_speed
func _physics_process(delta):
var collision = move_and_collide(velocity * delta)
if collision:
var n = collision.normal
velocity = velocity.bounce(n)
CollisionShape2D for the ball (circle shape)
Sometimes, after a collision the normal n isn’t perpendicular to the plane and he doesn’t have a magnitude of 1, wich is not OK for a normal
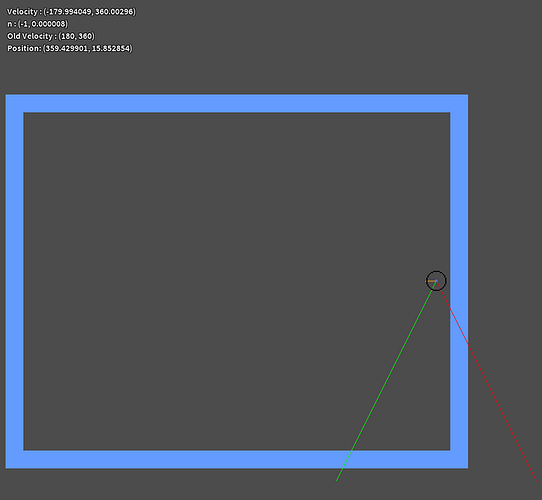
There is a screenshot just after a collision with the wall to the right (this wall is perpendicular to the x axis).
As you can see :
n.x = -1
n.y = 0.000008
n magnitude ≈ 1.000000000032
Not perpendicular to the right wall, since the right wall is perpendicular to the x axis. normal should be = <-1, 0>
Because of that the velocity isn’t the same after a bounce, sure I can round n up or down.
Sometimes the normal is ok, sometimes not. Why is that ?