Why is a (1, 1) vector longer than a (1, 0) vector?

Question

I understand how to get the length of a vector, and that (1, 1) calculates to longer than (1, 0). But why is this true conceptually? When I visualize a graph isn't (1, 1) the same distance from the point (0, 0) as (1, 0) is? Wouldn't a line drawn from (0, 0) to both vectors be the same length? Sorry not really Godot related but I thought about this when I normalized a diagonal movement vector.

Comments

You can think of a vector like a right angle triangle.

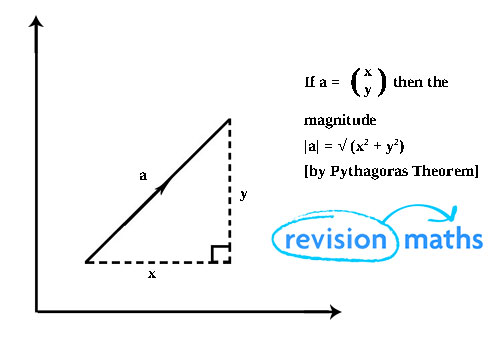
The x and y components are the lengths of the two shorter sides which are at right angles to eachother. The length (a) is the hypotenuse which joins the start of one component and the end of the other together.

You can use pythagoras' theorem to calculate the length of the hypotenuse.

For the (0,1) vector |a| = sqrt(1^2 + 0^2) = sqrt(1) = 1
So the length is 1

For the (1,1) vector |a| = sqrt(1^2 + 1^2) = sqrt(1 + 1) = sqrt(2)
So the lengt is sqrt(2) or about 1.41

Answer 1

If you draw a circle of radius 1 at the center point, and drawing a vector to position 1,1 it will clearly exceed the radius of the circle. In other words, it will have a length greater than one. Normalizing a vector means that its modulus or length always measures one, this means that rotating the vector in any direction will always be the size of the unit circle.